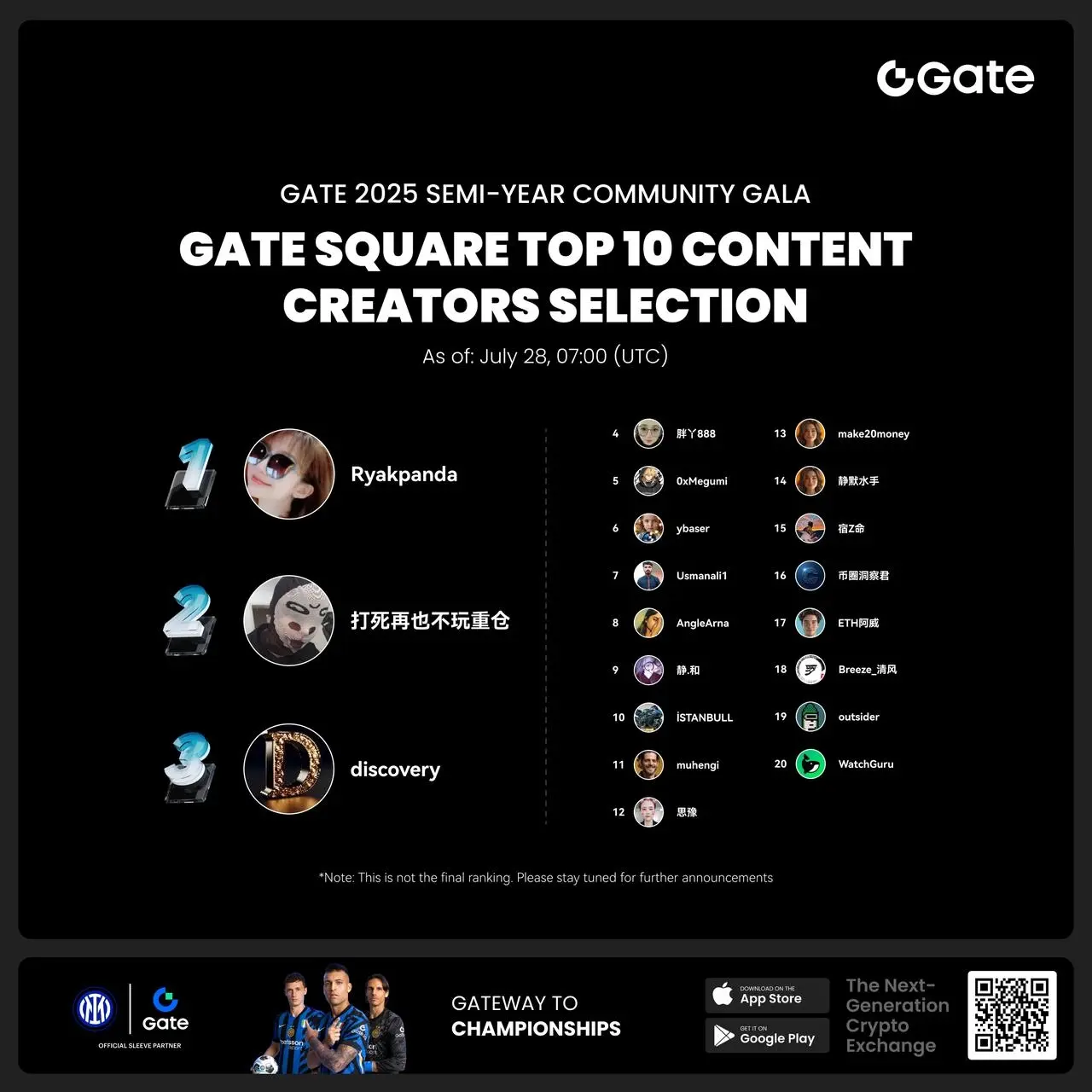
Google: Large models not only have the ability to emerge, but also have the ability to "comprehend" after a long training time

In 2021, researchers made an amazing discovery when training a series of miniature models, that is, after a long period of training, there will be a change in the model, from only "memorizing training data" at the beginning, to being able to understand what has never been seen before. The data also exhibit strong generalization capabilities.

This phenomenon is called "grokking". As shown in the figure below, after the model fits the training data for a long time, the phenomenon of "grokking" will suddenly appear.

Since the miniature model has this characteristic, will the more complex model suddenly appear "comprehension" after a longer training period? Recently, large language models (LLMs) have developed rapidly. They seem to have a rich understanding of the world. Many people think that LLMs are just repeating memorized training content. How true is this statement? How can we judge that LLMs are outputting memory content? , or does it generalize well to the input data?

In order to better understand this problem, researchers from Google in this article wrote a blog, trying to figure out the real reason for the sudden "comprehension" phenomenon of large models.

This article starts with the training dynamics of the miniature model. They designed a single-layer MLP with 24 neurons and trained them to learn to do the task of modular addition. We only need to know that the output of this task is periodic. of the form (a + b) mod n.

The weights of the MLP model are shown in the figure below. It is found that the weights of the model are very noisy at first, but as time increases, they begin to show periodicity.

This periodicity is even more apparent if the weights of individual neurons are visualized:

Don't underestimate the periodicity. The periodicity of the weights indicates that the model is learning a certain mathematical structure, which is also the key to the transformation of the model from memory data to generalization ability. Many people are confused by this transition, why the model changes from memorizing the data pattern to generalizing the data pattern.

Experiment with 01 sequence

To tell whether the model was generalizing or memorizing, the study trained the model to predict whether there was an odd number of 1s in the first three digits of a random sequence of 30 ones and zeros. For example, 000110010110001010111001001011 is 0 and 010110010110001010111001001011 is 1. This is basically a slightly trickier XOR problem with some interfering noise. If the model is generalizing, it should only use the first three digits of the sequence; if the model is memorizing the training data, it will also use subsequent digits.

The model used in this study is a single-layer MLP trained on fixed batches of 1200 sequences. At first, only the training accuracy improves, i.e. the model remembers the training data. As with modular arithmetic, test accuracy is stochastic in nature, rising sharply as the model learns a general solution.

Why this happens can be more easily understood with the simple example of the 01 sequence problem. The reason is that the model does two things during training: minimize loss and weight decay. The training loss actually increases slightly before the model generalizes, as it trades the loss associated with outputting the correct label for lower weights.

The sharp drop in test loss makes it look like the model is generalizing suddenly, but if you look at the model's weights during training, most models smoothly interpolate between the two solutions. Fast generalization occurs when the last weight connected to subsequent distracting digits is pruned through weight decay.

**When did the phenomenon of "comprehension" occur? **

It is worth noting that "grokking" is an accidental phenomenon - if the model size, weight decay, data size and other hyperparameters are not appropriate, the "grokking" phenomenon will disappear. If the weights decay too little, the model will overfit to the training data. If the weights decay too much, the model will not be able to learn anything.

Below, the study trains more than 1000 models on the 1 and 0 tasks using different hyperparameters. The training process is noisy, so nine models are trained for each set of hyperparameters. It shows that only two types of models have "comprehension" phenomenon, blue and yellow.

** Modular addition with five neurons **

Modulo addition a+b mod 67 is periodic, if the sum exceeds 67, the answer will produce a wrapping phenomenon, which can be represented by a circle. In order to simplify the problem, this study constructs an embedding matrix, using cos⁡ and sin⁡ to place a and b on the circle, expressed as the following form.

It turns out that the model finds the solution perfectly and accurately with only 5 neurons:

Looking at the trained parameters, the research team found that all neurons converged to roughly equal norms. If you plot their cos⁡ and sin⁡ components directly, they are basically evenly distributed on a circle.

next is

, which is trained from scratch with no built-in periodicity, the model has many different frequencies.

The study used the Discrete Fourier Transform (DFT) to separate out the frequencies. Just like in the 1s and 0s task, only a few weights play a key role:

The figure below shows that at different frequencies, the model can also achieve "comprehension":

Open Questions

Now, while we have a solid understanding of how single-layer MLPs solve modular addition and why it arises during training, there are still many interesting open questions in terms of memory and generalization.

**Which model is more constrained? **

Broadly speaking, weight decay can indeed guide various models to avoid memorizing training data. Other techniques that help avoid overfitting include dropout, downsizing models, and even numerically unstable optimization algorithms. These methods interact in complex nonlinear ways, so it is difficult to predict a priori which method will eventually induce generalization.

Also, different hyperparameters would make the improvement less abrupt.

**Why is memorization easier than generalization? **

One theory is that there may be many more ways to memorize the training set than generalize. Therefore, statistically, memorization should be more likely to happen first, especially in the case of no or little regularization. Regularization techniques such as weight decay favor certain solutions, for example, favoring "sparse" solutions over "dense" ones.

Research has shown that generalization is associated with well-structured representations. However, this is not a necessary condition; some MLP variants without symmetric inputs learn less "circular" representations when solving modular addition. The research team also found that a well-structured representation is not a sufficient condition for generalization. This small model (trained without weight decay) starts to generalize and then switches to using recurrently embedded memories.

As you can see in the figure below, without weight decay, the memory model can learn larger weights to reduce the loss.

It's even possible to find the hyperparameters where the model starts to generalize, then switch to memory, then switch back to generalize.

**What about larger models? **

Understanding the solution to modular addition is not trivial. Do we have any hope of understanding larger models? On this path you may need:

1. Train simpler models with more inductive bias and fewer moving parts.

2. Use them to explain puzzling parts of how larger models work.

3. Repeat as needed.

The research team believes this may be a way to better understand large models efficiently, and that over time, this mechanized approach to interpretability may help identify patterns that allow neural networks to learn Algorithmic revelation becomes easy and even automated.

For more details, please read the original text.

Original link: